L'ordonnancement du personnel de bord dans l'aviation n'est pas un problème facile. Il s'agit d'assigner des personnes à des vols en respectant une myriade de contraintes réglementaires (temps de travail, temps de pause… sans oublier les conditions négociées avec les syndicats), en trouvant suffisamment de personnes pour chaque vol (en fonction de la taille de l'avion et du nombre de passagers), en maximisant les bénéfices. Sans oublier que des imprévus peuvent arriver et que, même dans ces cas, certaines contraintes doivent toujours être respectées. À la moindre erreur, tous les vols d'une compagnie peuvent être affectés pendant plusieurs jours : c'est ce qui était arrivé à American Airlines l'an dernier. Ces problèmes sont, pour la plupart des compagnies aériennes, résolus par ordinateur, à l'aide de techniques d'optimisation poussées : optimisation en nombres entiers (MIP), programmation par contraintes (CP), heuristiques et algorithmes d'optimisation, toutes imbriquées les unes dans les autres pour profiter de tous leurs avantages en temps de calcul et en optimalité (pour trouver l'assignation qui réduit les coûts). L'amélioration continue des processeurs ces dernières décennies a été nécessaire pour garder des temps de calcul raisonnables avec l'augmentation du trafic aérien, mais elle ne sera probablement plus suffisante dans un futur proche.
Pour ces problèmes et d'autres, des chercheurs se penchent sur des solutions matérielles pour l'optimisation : concevoir des machines spécifiquement pour résoudre ce type de problèmes hautement combinatoires. L'informatique quantique pourrait être une solution, mais ce n'est pas la seule piste envisagée : les ordinateurs optiques pourraient apporter des bénéfices non négligeables.
En physique, Ernst Ising a longtemps étudié les moments magnétiques et leurs transitions, surtout les configurations où l'énergie est minimisée. Un aimant peut être vu comme une grille d'atomes en trois dimensions, chacun étant un "petit aimant". Les électrons de ces atomes peuvent être orientés dans n'importe quelle direction, ce que l'on appelle le spin. Les électrons de valence, situés à la périphérie de l'atome (ceux qui servent aux liaisons chimiques), ne peuvent avoir que deux spins différents : l'un pointe vers le haut, l'autre vers le bas. Si tous les électrons de valence de tous les atomes pointent dans le même sens, l'aimant est magnétisé dans ce cas ; au contraire, s'il règne un désordre complet dans ces orientations, l'aimant n'est pas magnétisé.
En termes d'énergie, deux électrons voisins ont une énergie combinée plus faible si leurs spins pointent dans des directions opposées, plus forte sinon (et ce n'est qu'une approximation : toute paire d'électrons peut interagir, dans un sens ou l'autre selon la paire, avec une intensité propre à cette paire). Le problème d'optimisation d'Ising correspond à la détermination de l'état où l'énergie totale du système est minimisée. À cause de toutes les interactions entre électrons, trouver cet état d'énergie minimale est très difficile pour un ordinateur.
En réalité, on peut prouver que ce problème est dans la classe de complexité NPC (NP-complete), ce qui indique que le modèle est très général : on peut transformer toute instance d'un problème de la classe NPC en un problème d'optimisation d'Ising.
Bienvenue dans le monde de l'optimisation quantique adiabatique !
Reste maintenant à transformer un problème d'optimisation classique sous la forme d'un problème d'Ising… et à résoudre ce dernier, avec l'aide de la physique. Vu qu'il est assez difficile de travailler avec des spins, bon nombre de chercheurs préfèrent travailler avec de la lumière, plus précisément des impulsions ; ces impulsions peuvent également interagir entre elles, comme les spins. On peut alors mesurer l'énergie totale du système, puis tenter de modifier les impulsions pour la diminuer.
L'élément de base du prototype de l'université de Stanford pour la correspondance entre un spin et une impulsion de lumière est un oscillateur optique paramétrique (OPO), un appareillage qui ressemble à un laser. La différence principale est que la lumière produite est exactement soit en phase, soit en opposition de phase par rapport à une lumière de référence : c'est ainsi que le spin est représenté (spin vers le haut quand les deux sont en phase, vers le bas sinon).
L'histoire débute avec une source de lumière, un laser pulsé capable de produire des impulsions de quelques picosecondes. Celui-ci en émet deux, dans deux directions différentes : une lumière de référence et une source d'énergie pour l'OPO. Cette impulsion traverse un cristal situé dans l'OPO, qui se met à produire d'autres impulsions. Ces dernières sont envoyées dans une bobine de fibre optique de plusieurs centaines de mètres de long : elle stocke toutes les impulsions, qui se propagent le long de la fibre optique avant de repasser dans le cristal et d'être à nouveau injectées dans la fibre optique. Au début, quand une impulsion est créée, elle n'a pas une intensité très élevée : il lui faut plusieurs passages dans la boucle, chacun lui permettant d'interagir avec d'autres impulsions ; toutes ces interactions finissent par définir la phase de l'impulsion.
C'est à ce moment qu'intervient de l'électronique plus basique. Dans la boucle, une petite partie de l'énergie des impulsions est déviée et comparée avec l'impulsion de référence à l'aide d'un détecteur homodyne. Cette information est numérisée et traitée dans un processeur classique, c'est là que le problème d'Ising est représenté. Pour chaque impulsion (ou chaque spin), ce dernier détermine l'impact que chaque autre impulsion devrait avoir sur la première impulsion.
Alors, un calcul sophistiqué détermine la phase, l'intensité et le moment où il faut changer l'impulsion de référence pour que la combinaison se fasse avec la bonne impulsion dans l'OPO afin de diminuer l'énergie totale du système. L'impulsion stockée se rapproche alors d'un spin orienté vers le haut ou le bas.
Après une dizaine ou une centaine d'itérations, toutes les impulsions finissent par trouver leur phase finale. À partir de ce moment, un ordinateur lit les phases de chaque impulsion, les traduits en termes de direction de spin, puis en solution au problème d'optimisation à résoudre.
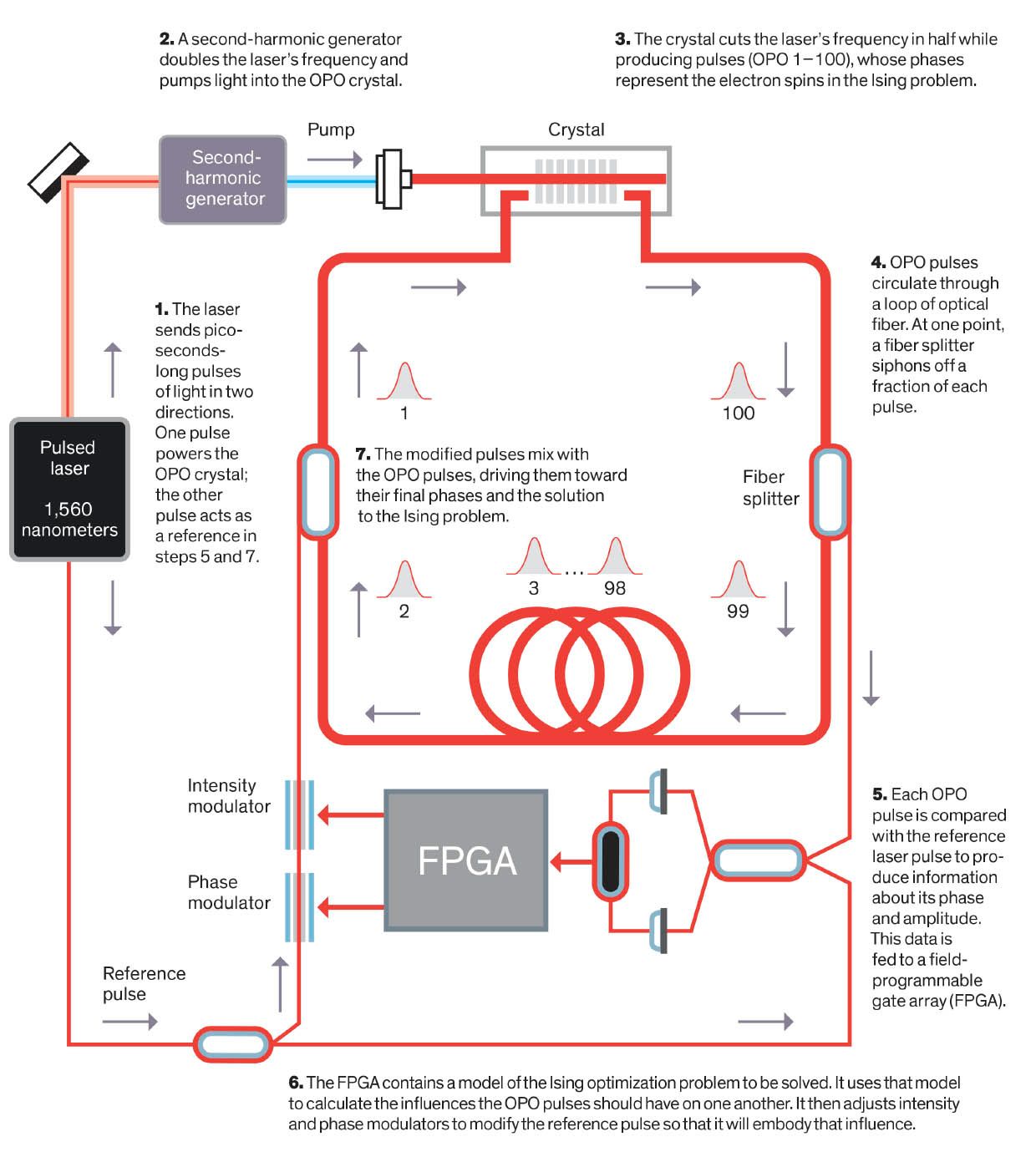
Ce système n'en est encore qu'à l'état de prototype, mais il a pu résoudre des problèmes faisant intervenir cent spins. Cette machine semble converger mieux que d'autres systèmes optiques similaires, y compris ceux développés à la NASA, même si la recherche n'est pas finie dans ce domaine.
Source et images : To Crack the Toughest Optimization Problems, Just Add Lasers.